- Topic1/3
11k Popularity
14k Popularity
16k Popularity
5k Popularity
21k Popularity
- Pin
- #Gate 2025 Semi-Year Community Gala# voting is in progress! 🔥
Gate Square TOP 40 Creator Leaderboard is out
🙌 Vote to support your favorite creators: www.gate.com/activities/community-vote
Earn Votes by completing daily [Square] tasks. 30 delivered Votes = 1 lucky draw chance!
🎁 Win prizes like iPhone 16 Pro Max, Golden Bull Sculpture, Futures Voucher, and hot tokens.
The more you support, the higher your chances!
Vote to support creators now and win big!
https://www.gate.com/announcements/article/45974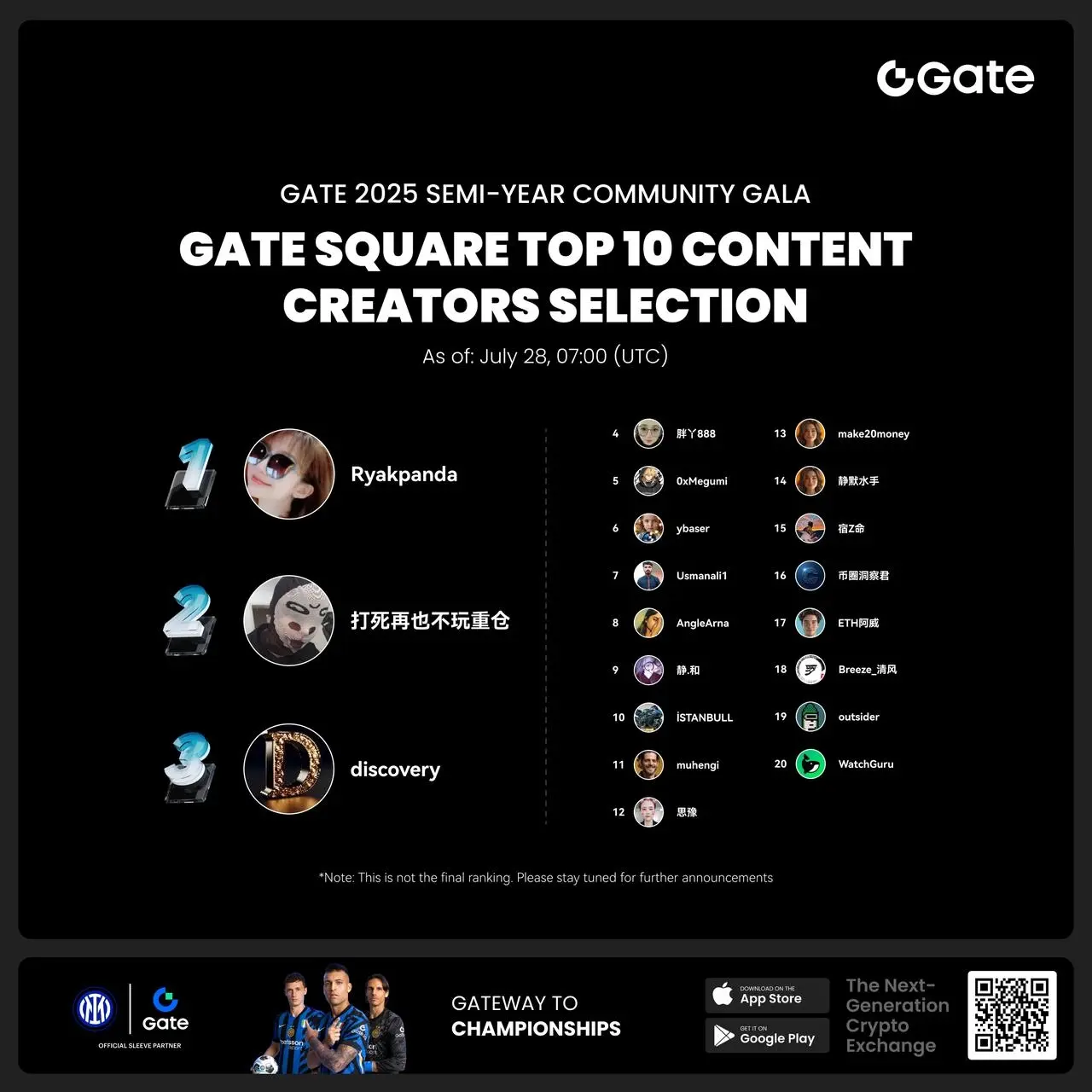
- 🎉 Hey Gate Square friends! Non-stop perks and endless excitement—our hottest posting reward events are ongoing now! The more you post, the more you win. Don’t miss your exclusive goodies! 🚀
1️⃣ #ETH Hits 4800# | Market Analysis & Prediction: Boldly share your ETH predictions to showcase your insights! 10 lucky users will split a 0.1 ETH prize!
Details 👉 https://www.gate.com/post/status/12322612
2️⃣ #Creator Campaign Phase 2# |ZKWASM Topic: Share original content about ZKWASM or its trading activity on X or Gate Square to win a share of 4,000 ZKWASM!
Details 👉 https://www.gate.com/post/st
Decentralized Finance Innovation: An Analysis of the Application and Challenges of Multiple Recursive Operators
The Application and Challenges of Multiple Recursive Operators in Decentralized Finance
The concept of algorithmic stablecoins has attracted the attention of many people, with many believing that it may achieve the goal that Bitcoin has failed to accomplish: a completely decentralized and self-adjusting global currency. The emergence of this idea is not only due to a lack of in-depth understanding of blockchain and currency, but also related to the new type of recursive operator introduced by algorithmic stablecoins. This novel recursive operator has created expectations for "breakthrough innovation."
A recursive operator refers to an operation in continuous transformations of smart contracts, where the previous state is used as input and looped repeatedly to generate the next state. In a blockchain environment, the public nature of data and the serial design of smart contracts form a time series. Recursively processing similar operations can produce nonlinear structures and even geometric series effects. This strong positive feedback characteristic highly aligns with the self-enhancing properties of on-chain games, making it an ideal choice for exploring the possibilities of new types of non-cooperative games.
However, simple time series recursion is not ideal, as it makes the future state completely determined by the current state. What is truly valuable is to combine recursive operators with other elements, introducing new information during the state transition process. This information reflects game characteristics and possesses unpredictability. This unpredictability is also influenced by the recursive operators, forming certain common expectations, which in turn affect other operators, creating a controllable expectation attribute. We refer to this type of operator as a multiple recursive operator.
Taking a simple algorithmic stablecoin as an example, the pricing operator generates the price Pt, while the total supply Mt is a multiple recursive operator. Mt is a function of Pt, and Pt+1 depends on Mt, thereby establishing an indirect recursive relationship between Mt+1 and Mt. With the cooperation of the pricing operator, a periodic negative feedback loop is formed, gradually tending towards price stability. This design is based on the equilibrium of the supply and demand curve, and the game process occurs in the secondary market, so it is not very precise, which may lead to a slow transmission process and difficulty in forming a stable equilibrium.
Recursive operators can provide not only negative feedback but also positive feedback. For example, the buyback mechanism in a certain system is a typical positive feedback recursive operator: buybacks reduce market supply, drive up prices, enhance system performance, meet more demand, generate more revenue, and further increase buybacks, creating a virtuous cycle. This straightforward and clear method with anti-Markov properties may attract more attention from on-chain protocol developers.
From a purely mathematical perspective, it remains unclear whether recursive operators can construct stable short-cycle attributes. Therefore, stablecoins that rely on recursive operators find it difficult to converge to a stable structure. This is especially true considering that algorithmic stablecoins indirectly affect supply and demand relationships by changing the total amount, which results in a slower transmission and more constraints to reach a stable equilibrium, making it more challenging to achieve their own goals.
In multiple recursive operators, the step of introducing new information is crucial. The general equilibrium properties of blockchain indeed make it easy to incorporate more information, which has a certain degree of uncertainty under the design of the game structure, yet possesses a framework of unified information structure. This information, when combined with recursive operators, establishes a holistic expectation that can easily create an illusion of stability. Without a rigorous game-theoretic analysis, it is difficult to fully grasp the overall equilibrium properties, which may be contrary to expectations.
Sometimes there is a need for randomness in the process of introducing information. This assumption of randomness has zero dependence on the information, and when combined with recursive operators, it may actually be easier to produce stable traits. This randomness, which is detached from game structures and more reflective of algorithmic characteristics, may be a direction that future algorithmic stablecoins need to explore.
When designing Decentralized Finance, if the goal is to strengthen positive and negative feedback, the frequency of introducing new information needs to be reduced. If the goal is to pursue long-cycle regression, then the introduction of information flow itself should also possess certain cyclical properties. Proving that a random operator can achieve regression under the designed recursive operator is a challenging task.
In the field of Decentralized Finance, most recursive operators will combine with price sequences, as price games are the form of competition where information is most concentrated and difficult for algorithms to predict or control. However, most designs currently do not rely on effective decentralized oracles, but instead depend on the AMM mechanism, which may lead the recursive process to become deterministic or controllable, contrary to the original intention of the recursive operator design.
In addition, the recursive amounts designed by many projects are not directly linked to the supply and demand variables that determine the price sequence, but are related to the total amount of assets. This may lead to an inability to directly reach the core of the game in the secondary market, and the transmission of operators may deviate.
In the future, we should explore more combinations of variables and recursive operators, especially parameters that reflect the difficulty of market-wide games. When designing Decentralized Finance, a detailed analysis of the information transmission mechanism of recursive operators should be conducted to avoid being predicted and controlled. There is still a large series of nonlinear operators in this field that are worth exploring in depth.